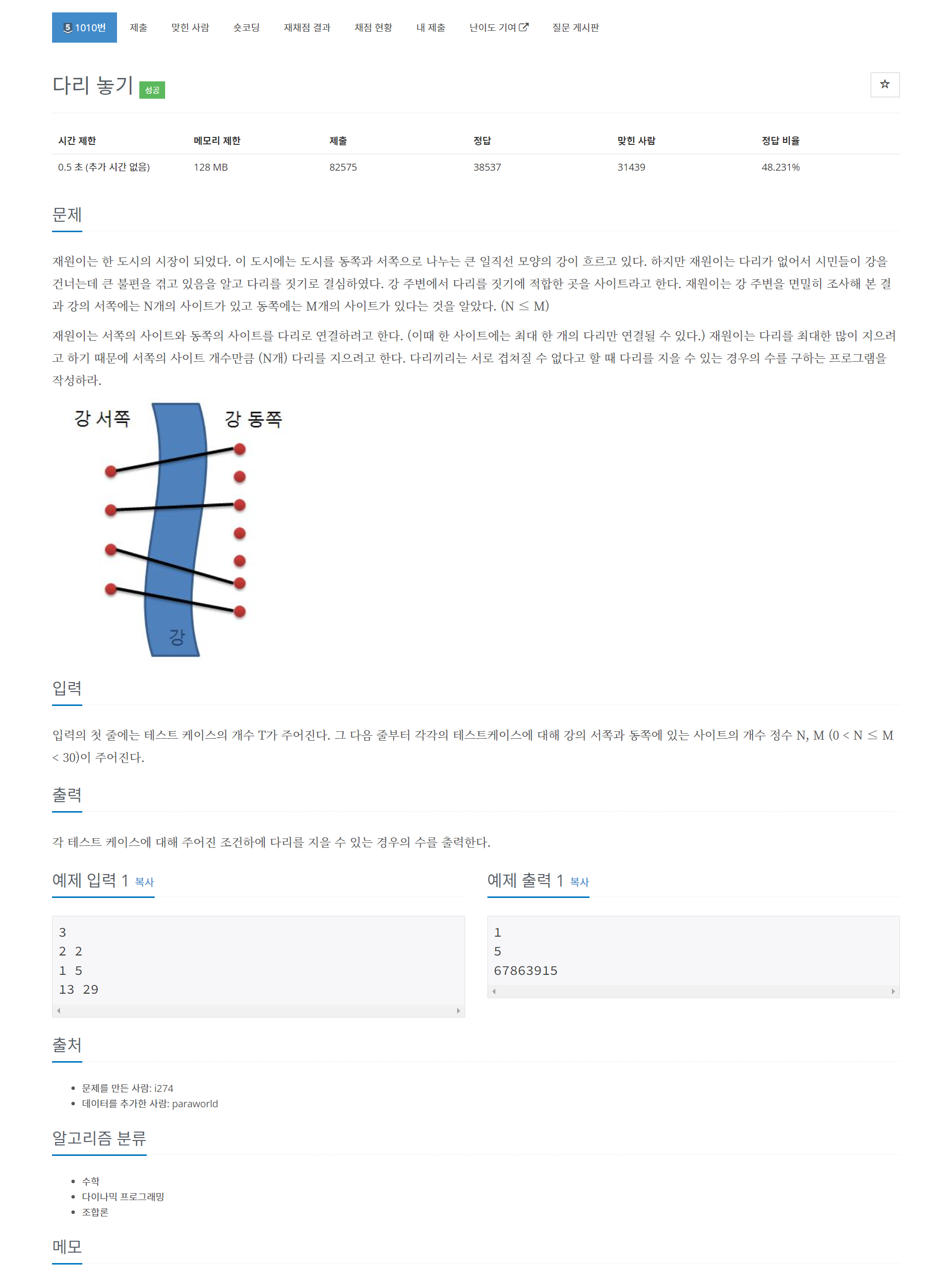
문제
1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
풀이
조합 공식을 이용하면 된다. 동쪽이 서쪽에 비해 더 많거나 같은 사이트를 가지고 있기 때문에 동쪽 M개에서 서쪽 N개 중 하나를 고르는 조합인 $_{M}C_{N}$을 구하면 된다.
$_{M}C_{N}$을 구하는 조합 공식은 아래와 같다.

위의 공식으로 팩토리얼 값을 계산하여 풀이할 수도 있지만, 이 문제는 조합의 성질을 이용해 점화식을 만들고 dp로 풀이할 수 있다.


위의 두 가지 성질을 이용해 점화식을 세울 수 있고, 이 성질들은 파스칼 삼각형으로 쉽게 이해할 수 있다.

위의 이미지는 파스칼의 삼각형을 설명해준다. 파스칼 삼각형을 이항 계수를 삼각형 모양으로 나열한 것으로 삼각형 속의 숫자는 바로 윗 줄에 인접하는 두 숫자의 합으로 정의된다. 그리고 이는 조합으로 증명할 수 있다. $_{n}C_{r}$에서 n 중에 한가지를 A라고 할 때, A가 포함되는 경우와 A가 포함되지 않는 경우로 나눌 수 있다. 전자의 경우에는 n - 1 중에서 r - 1을 고르면 되므로 $_{n-1}C_{r-1}$ 이고, 후자의 경우에는 나머지 n - 1개 중에서 r개를 고르면 되므로 $_{n-1}C_{r}$이 되는 것으로 식으로 나타내면 아래와 같다.

따라서 위의 두가지 성질을 이용해 점화식을 만들면 된다. 2차원 dp 배열을 선언하고 이를 파스칼 삼각형처럼 사용하기 위해, 배열의 순번마다 앞과 끝은 1로 만들고 그 사이의 숫자는 윗 줄의 합으로 정의하면 된다. 만들어진 점화식은 dp[i][0] = 1, dp[i][i] = 1 과 dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] 이 된다.
코드
import java.util.*
fun main() {
val br = System.`in`.bufferedReader()
val bw = System.out.bufferedWriter()
val dp = Array(31){ IntArray(31) }
for(i in 1 .. 30) {
dp[i][i] = 1
dp[i][0] = 1
}
for(i in 2..30) {
for (j in 1..30) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
}
}
val sb = StringBuilder()
val testCase = br.readLine().toInt()
repeat(testCase) {
val st = StringTokenizer(br.readLine())
val (west, east) = arrayOf(st.nextToken().toInt(), st.nextToken().toInt())
sb.append("${dp[east][west]}\n")
}
bw.write("$sb")
bw.flush()
bw.close()
br.close()
}
'알고리즘 > Baekjoon' 카테고리의 다른 글
| [백준] 11401번: 이항 계수 3 - Kotlin[코틀린] (0) | 2023.09.18 |
|---|---|
| [백준] 11051번: 이항 계수 2 - Kotlin[코틀린] (0) | 2023.09.17 |
| [백준] 10814번: 나이순 정렬 - Kotlin[코틀린] (0) | 2023.08.10 |
| [백준] 1149번: RGB거리 - Kotlin[코틀린] (0) | 2023.08.07 |
| [백준] 10773번: 제로 - Kotlin[코틀린] (0) | 2023.08.07 |